I am looking for a method to reproduce the feature of oscillator syncing. For example,
if osc1 phase == 0 then force osc2 phase=0
The above makes sense if osc1 and osc2 produce signals at different frequencies.
I use vco2 opcode for both oscillators.
I do not know if this problem can be solved and how…
I’m not sure how you can do this with a vco2 opcode. The http://www.csounds.com/manual/html/syncphasor.html and https://csound.com/docs/manual/oscilikts.html opcodes might be useful. You may need to use them with https://csound.com/docs/manual/vco2ft.html to avoid aliasing.
Thank you. I need to study these opcodes. I was thinking that
kphase phasor p4
is synced with the output of
aosc1 vco2 p5, p4
and can be used as a phase indicator.
then I need to force
aosc2 vco2 p5, freq2, 2, kpw, 0
If I do this as action following a condition (if kphase==0 then)…
what happens to the phase of aosc2 when the next a-cycle is calculated ??
I assume it will return to 0, but you would need to run this in an instrument where ksmps is 1? I’m not sure how efficient it will be.
Good new and bad news.
I got results with the following code. The audio clips whenever the 2nd oscillator is forced to phase=0
(the print command assured me that clipping is associated with phase correction)
aO1 poscil p5, p4
kphase phasor p4
if kphase < 0.0025 then
aO2 poscil p5, p4*1.02, -1, 0
printk2 kphase
else
aO2 poscil p5, p4*1.02
endif
display aO2, (16/p4) ,1
And I was able to capture it, but I am not sure what I see here.
and here…
This is what I’d expect to see. Resetting the phase during a cycle is bound to create discontinuities in the signal. I’m not well versed in oscillator syncing, but I guess this type of ‘hard sync’ is quite likely to produce such results?
I did it! But I do not understand the code. I do not understand how it works. I do not understand why the syncing is executed at the proper time (variable itime) and the rest of the signal is calculated with incremental phase.
aO1 poscil p5, p4
itime = 1 / p4
reset:
timout 0, itime, contin
reinit reset
contin:
aO2 poscil p5, p4*1.02, -1, 0
rireturn
display aO2, (16/p4) ,1
then aO2 looks like this:
Since aO2 has a higher pitch, its cycle is a few samples less than aO1. So, the aO2 signal starts the new cycle sooner than aO1 and then the aO2 phase drops to 0 in order to be synced with aO1. That is what I expected to be “syncing osc2 to osc1”
BTW, no clipping!!
Note: The extra arguments of aO2 are not required. aO2 poscil p5, p4*1.02 also does the job correctly.
Unfortunately, the above solution alters the pitch of aO2 even for ksmps as low as 4. The best performance is for ksmps=1 as Rory predicted.
The purpose of syncing is to alter the timbre, not the pitch. In Fred Welsch’s words: “the slave will take on a thin, brittle timbre , however the overall pitch stays the same.”
I am afraid that I have to forget a wave and FFT display at the same time… 
I imagine this is the reason why opcodes for written for this task.
Unfortunately, variable itime of timeout opcode fails to respond in real time when the instrument orc code is a bit more complicated as in a subtractive synth emulation in csound.
I am going to try again using the various phasors. The first try was unsuccessful. Unfortunately the phase variable of the involved opcodes run in different mode.
aphase, asyncout syncphasor xcps, asyncin, iphs
ares poscil kamp, kcps, -1, iphs
ares vco2 kamp, kcps [, imode] [, kpw] [, kphs] [, inyx]
So, doI have to read an a-phase with vaget to turn it to a k-phase and then use reinit to turn it to an i-phase ??? Well, it didn’t work. I must find another way to do it.
I’m not sure but I think the idea with this movie is too drive a table reading opcode. This opcode produces an upward saw with can be fed directly to a table opcode. At least that’s my take on it…
It seems that the correct code is as simple as that:
aO1 poscil3 p5,p4
anosync init 0.0
aO1ph, async syncphasor p4, anosync
ksync vaget 0, async
if ksync==1 then
reinit phase
endif
phase:
aO2 poscil3 p5, p4 * 1.05
rireturn
display aO2, (8/p4)
The signal produced is this:
async is a trigger that turns to 1 whenever the phase of syncphasor crosses zero.
vaget turns the a-value to k-value.
The rest of the mechanism is similar to the timeout example I used before.
Now… we are still at ksmps = 1 and during the weekend I am going to test my discovery with the subtravtive synth I am building.
It seems that rireturn is “executed” only when a reinit preceeds it (in this case, inside the “if statement” Without a reinit the command has no effect to the code.
I would have thought the entire point of these syncing opcodes is too avoid having to use reinit at all…
Maybe search through the Cabbage examples, @iainmccurdy might have some examples of oscillator syncing?
CZSynth by Ian McCurdy uses the reinit command (line 231) in the same fashion as I do.
What are your concerns about reinit ?
for example a) executes an i-task during a k-pass ? b) because of ksmps=1 ? (CZSynth runs at ksmps=16) or c) it jumps out of the ‘if-block’ without reaching endif ?
I would avoid using any oscil-class opcode and use table-class ones instead.
A basic hard-sync oscillator scheme is attached. Two syncphasors are used. In the first syncphasor, the sync-in is ignored (its sync-out is used though). In the second syncphasor, its sync-out is not used, but its phase (sync-in) will be forced-reset by the sync-out from the first syncphasor.
The jump back to phase=0 will cause a discontinuity and ugly buzzing, but a way to prevent this is to apply a windowing envelope which follows the phase of the first oscillator. In this example I used a half-sine as the window.
hardsyncOscillators.csd (1.0 KB)
Rather than call them ‘master’ and ‘slave’, I call the oscillator that determines the pitch, the fund(amental). The other sounds like a bandpass filter applied to the first so I call it form(ant).
Good morning! Thank you very much for the support. I am going to study your example as well as the Cabbage example HardSyncSynth.Unfortunately I have not worked with ftgen and tablei opcodes, so a period of customization to the new (for me) material is required.
I hope to improve a basic disadvantage of my code: It consumes tooooo much of CPU resources compared to KONTAKT or FL Studio’s soundfont player.
Yet, I am proud to announce that I have uploaded my work (so far) to github, and looking forward to return to the hard sync problem as soon as I am able.
It sounds like you are making progress, but the heavy CPU drain should be fixable.
If you are interested in hard-sync oscillator-like sounds, you should also investigate synchronous granular synthesis. I’ve attached a basic example using the grain3 opcode. This will offer a range of advantages and options - I’ve added one: a resonance control.
SyncGran.csd (1.7 KB)
In your example hardsyncOscillators.csd
Can you please explain to me the line
a2 tablei aphase2,-1,1,0,1
I am a bit confused with the -1, and the wrap around.
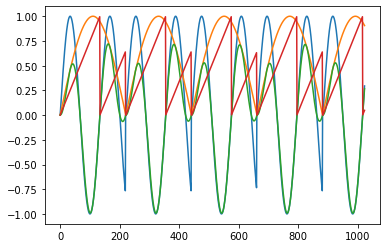
I have created a “test-tube” with python and ctcsound in order to visualize your HardSyncOscillator example. I really try to understand the importance of the envelope. (As if you are trying to eliminate clicks…) Anyway, I am encouraged to use the technique myself, as it works in ksmps = 32.
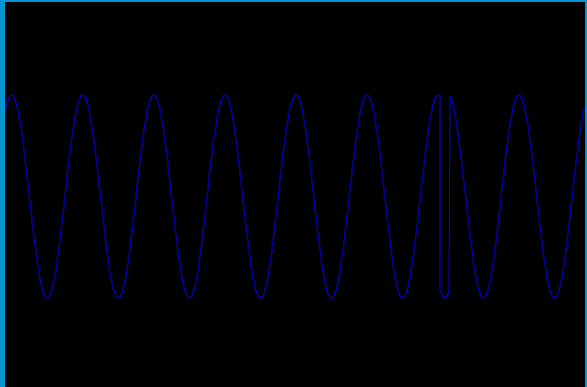
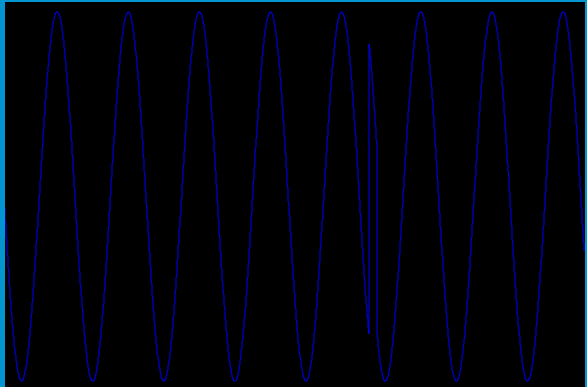
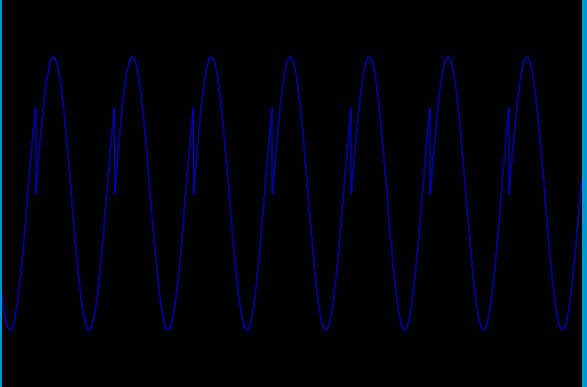
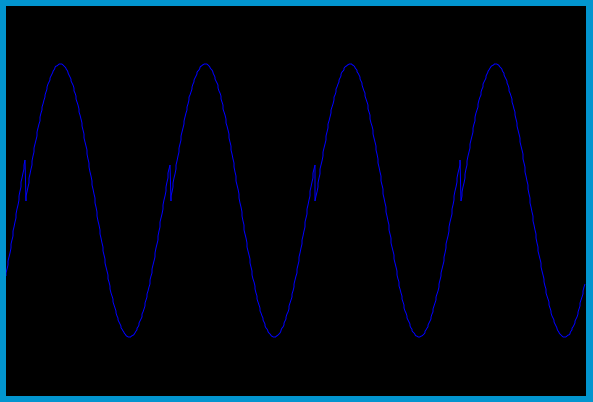
These are the first 1024 audio samples. 32 cycles times 32 samples per cycle (ksmps=32).
a2 = blue, aEnv = yellow, aout = green, and phase2 = red
More interesting is the python code I wrote. Could be useful to anyone.
import ctcsound
import numpy as np
from matplotlib import pyplot as plt
ach1 = []
ach2 = []
ach3 = []
aph = []
orc_text = '''
ksmps = 32
nchnls = 2
0dbfs = 1
giHalfSine ftgen 0,0,4097,9,0.5,1,0
instr 1
kFreq1 chnget "freq1"
kFreq2 chnget "freq2"
aphase1,asyncout1 syncphasor kFreq1, a(0)
aphase2,asyncout2 syncphasor kFreq2, asyncout1
a1 tablei aphase1, -1,1,0,1
a2 tablei aphase2,-1,1,0,1
aEnv tablei aphase1,giHalfSine,1
aout = a2 * aEnv
chnset a2, "ch1"
chnset aEnv, "ch2"
chnset aout, "ch3"
chnset aphase2, "cph"
outs aout,aout
endin
'''
sco_text = "i 1 0 5"
cs = ctcsound.Csound()
cs.setOption("-d")
cs.setOption("-odac")
cs.compileOrc(orc_text)
cs.readScore(sco_text)
cs.start()
cs.setControlChannel("freq1", 200)
cs.setControlChannel("freq2", 330)
i=0
while cs.performKsmps()==False and i<32:
atemp1 = cs.channelPtr("ch1", ctcsound.CSOUND_AUDIO_CHANNEL)
ach1 = np.append(ach1, atemp1[0])
atemp2 = cs.channelPtr("ch2", ctcsound.CSOUND_AUDIO_CHANNEL)
ach2 = np.append(ach2, atemp2[0])
atemp3 = cs.channelPtr("ch3", ctcsound.CSOUND_AUDIO_CHANNEL)
ach3 = np.append(ach3, atemp3[0])
atemp4 = cs.channelPtr("cph", ctcsound.CSOUND_AUDIO_CHANNEL)
aph = np.append(aph, atemp4[0])
i += 1
fig, ax = plt.subplots()
ax.plot(ach1)
ax.plot(ach2)
ax.plot(ach3)
ax.plot(aph)
cs.cleanup()
cs.reset()
del cs
I assume it’s to limit any clipping that might take place when the phase abruptly jumps back to 0? Nice use of ctcsound btw, it’s such a powerful package.